![[ html: Kepler III. törvénye https://hu.wikipedia.org/wiki/Kepler-t%C3%B6rv%C3%A9nyek#III._t%C3%B6rv%C3%A9ny ]](../_/html.gif)
 kivonom Newton I. törvényét
kivonom Newton I. törvényét
![[ html: Newton I. törvénye https://hu.wikipedia.org/wiki/Newton_t%C3%B6rv%C3%A9nyei#Newton_I._t%C3%B6rv%C3%A9nye_%E2%80%93_a_tehetetlens%C3%A9g_t%C3%B6rv%C3%A9nye ]](../_/html.gif)
 , megkapom Gay-Lussac II. törvényét
, megkapom Gay-Lussac II. törvényét
![[ html: Gay-Lussac II. törvénye https://hu.wikipedia.org/wiki/Gay-Lussac-t%C3%B6rv%C3%A9ny#Ide%C3%A1lis_g%C3%A1z_izochor_%C3%A1llapotv%C3%A1ltoz%C3%A1sa_(1802) ]](../_/html.gif)
 .
Newtonnak 4 törvénye van, míg Ohmnak csak egy, ebből is látszik, hogy Newton 6 decibellel nagyobb tudós Ohmnál.
Ha már Ohm, figyelmedbe ajánlom az Ohm Sweet Ohm nótát
.
Newtonnak 4 törvénye van, míg Ohmnak csak egy, ebből is látszik, hogy Newton 6 decibellel nagyobb tudós Ohmnál.
Ha már Ohm, figyelmedbe ajánlom az Ohm Sweet Ohm nótát
![[ html: Kraftwerk Ohm sweet Ohm https://www.google.com/search?q=kraftwerk+%22ohm+sweet+ohm%22 ]](../_/html.gif)
 .
.
Mutattam már áramkört, alkatrészeket összekapcsolva, de van két egyszerű szabály, törvény, aminek használata jelentősen megkönnyíti életedet.
Egy csomó hurokról lesz szó ( előbb-utóbb ).
Legalábbis én így jegyeztem meg, ugyanis a tanaraknak mániájuk egy tudós törvényeit megsorszámozni.
Lehetőleg római számokkal.
Logikus, hiszen ha Kepler III. törvényéből
![[ html: Kepler III. törvénye https://hu.wikipedia.org/wiki/Kepler-t%C3%B6rv%C3%A9nyek#III._t%C3%B6rv%C3%A9ny ]](../_/html.gif)
 kivonom Newton I. törvényét
kivonom Newton I. törvényét
![[ html: Newton I. törvénye https://hu.wikipedia.org/wiki/Newton_t%C3%B6rv%C3%A9nyei#Newton_I._t%C3%B6rv%C3%A9nye_%E2%80%93_a_tehetetlens%C3%A9g_t%C3%B6rv%C3%A9nye ]](../_/html.gif)
 , megkapom Gay-Lussac II. törvényét
, megkapom Gay-Lussac II. törvényét
![[ html: Gay-Lussac II. törvénye https://hu.wikipedia.org/wiki/Gay-Lussac-t%C3%B6rv%C3%A9ny#Ide%C3%A1lis_g%C3%A1z_izochor_%C3%A1llapotv%C3%A1ltoz%C3%A1sa_(1802) ]](../_/html.gif)
 .
Newtonnak 4 törvénye van, míg Ohmnak csak egy, ebből is látszik, hogy Newton 6 decibellel nagyobb tudós Ohmnál.
Ha már Ohm, figyelmedbe ajánlom az Ohm Sweet Ohm nótát
.
Newtonnak 4 törvénye van, míg Ohmnak csak egy, ebből is látszik, hogy Newton 6 decibellel nagyobb tudós Ohmnál.
Ha már Ohm, figyelmedbe ajánlom az Ohm Sweet Ohm nótát
![[ html: Kraftwerk Ohm sweet Ohm https://www.google.com/search?q=kraftwerk+%22ohm+sweet+ohm%22 ]](../_/html.gif)
 .
.
Vannak az emberek által létrehozott törvények és vannak a természeti törvények.
Az emberi törvényekről mindig lehet tudni, léteznek-e, hatályosak-e és mi a tartalmuk. Például Balatonfüred 18/2018. ( VII. 9. ) rendelete létezik, amikor ezt írom hatályos és a füredi Balaton-parton megtiltja a segwayezést. Megszegője 150 ezer forintig közigazgatási bírságolható. Ugyanakkor nem biztos, hogy a valóság megfelel a törvénynek. Előfordulhat, hogy valaki segwayezik a tiltott területen, de semmilyen eljárás nem indul ellene. Az emberi törvényről lehet tudni van-e és mi, de nem mindig működik.
Emberi törvény az is, amiről kitalálója azt állítja, hogy képzeletbeli barátja sugallta neki.
A természeti törvény sehová nincsen leírva, nem lehet tudni, van-e és miről szól. Az emberek megfigyelik a valóságot és ha valami sokszor ugyanúgy történik, akkor azt mondják: ez a törvény. A töltésmegmaradás törvénye is így törvény. Másrészt nincs kivétel a természeti törvény alól. Ha mégis másképp működik a valóság, mint a természeti törvény, akkor az emberek által megállapított törvény rossz és nem is az a valódi törvény. A természeti törvényről nem lehet tudni van-e, de ha van, akkor mindig teljesül.
Ajánlom Lukács Béla
![[ html: Lukács Béla https://hu.wikipedia.org/wiki/Luk%C3%A1cs_B%C3%A9la_(fizikus) ]](../_/html.gif)
 A természeti törvények evolúciója
A természeti törvények evolúciója
![[ html: Lukács Béla A természeti törvények evolúciója https://www.google.com/search?q=Luk%C3%A1cs+B%C3%A9la+A+term%C3%A9szeti+t%C3%B6rv%C3%A9nyek+evol%C3%BAci%C3%B3ja ]](../_/html.gif)
 című előadását ( is ).
című előadását ( is ).
Természeti törvényt ismerni jó dolog. Ismeretével meg tudok tervezni valamilyen hasznos kütyüt. ( Ha nem hibáztam, működni fog. ) A kütyü vagy közvetlenül nekem hasznos, vagy valaki másnak hasznos, aki pénzt ad érte, ami nekem ( is ) hasznos. Természeti törvényt ismerni jó dolog.
Tapasztalati tény, hogy az elektromos töltés megmarad.
Nem úgy, hogy van az Univerzumban valamennyi negatív töltés, és soha nem volt van lesz több vagy kevesebb.
Lehet, de ugyanannyival változik a pozitív töltés mennyisége.
Persze például egy
neutron ( 0 Qp ) elbomolhat egy
protonra ( +1 Qp ) és egy
W--ra ( -1 Qp ), ami hirtelen tovább egy
elektronra ( -1 Qp ) és
elektron-antineutrínóra ( 0 Qp )
( Qp = -Qe )
![[ html: Béta-bomlás https://hu.wikipedia.org/wiki/B%C3%A9ta-boml%C3%A1s ]](../_/html.gif)
 .
.
Ez már megint keveseket érdekel, a lényeg, hogy az össztöltés megmarad. Elektron, proton töltése sem változik meg hirtelen felindulásból. Nincs élmunkás elektron, aminek nagyobb a töltése, töltése nem inflálódik és nincs töltés nélküli sem. Ha a reggeli kávémban váratlanul megmanifesztálódna csak egy porszemnyi elektron, szétrobbanna. Házzal együtt. Mivel ilyen nem szokott előfordulni, az emberek úgy gondolják, hogy van egy töltésmegmaradási törvény.
A töltésmegmaradás egyik következménye, hogy egy vezeték minden pontján azonos az áramerősség.
( Most ideális vezeték, keresztmetszetét elhanyagolom, egyenáram, stb. )
Ugyanis, ha a vezeték egy pontjában keletkezik egy szóló elektron, akkor a potenciálkülönbség miatt nem marad a fenekén, hanem csatlakozik a többi elektron áramlásához.
A keletkezés pontját kijelölöm csomópontnak.
Mintha a Sajószentpéter melletti körforgalomból

![[wikimapia: 48.203397 20.738427]](../_/wikimapia.png)
 , aminek egy ki- és egy bejárata volt, több elektromos Trabant menne ki, mint amennyi be.
, aminek egy ki- és egy bejárata volt, több elektromos Trabant menne ki, mint amennyi be.

A csomópont után nagyobb/kisebb áramerősséget lehetne mérni mint előtte. Tapasztalat szerint ilyen nincs, a vezeték minden pontján ( keresztmetszetén ) azonos az áramerősség.
A kifolyó és a befolyó áramerősség akkor is megegyezik, a több ágra bomolva folyik ki vagy több ágról folyik be.
Egy csomópontól kifolyó áramok összege megegyezik az oda befolyó áramok összegével.
Beatrice rockzenekar 8 óra munka örökbecsű szövege szerint "ami befolyik az rögtön kifolyik".
![[ html: Beatrice 8 óra munka https://www.google.com/search?q=beatrice+8+%C3%B3ra+munka ]](../_/html.gif)
 Előző megfogalmazásokban különválogattam a kifolyó és a befolyó áramokat, így kezeltem irányukat.
Előfordulhat, hogy előre a franc se tudja, egy vezetéken merre fog folyni az áram.
Ekkor a kifolyó ( vagy a befolyó ) áramirányt kijelölnöm pozitívnak (, a másik irány negatív lesz ).
Így a törvény rendkívül elegáns lesz:
Előző megfogalmazásokban különválogattam a kifolyó és a befolyó áramokat, így kezeltem irányukat.
Előfordulhat, hogy előre a franc se tudja, egy vezetéken merre fog folyni az áram.
Ekkor a kifolyó ( vagy a befolyó ) áramirányt kijelölnöm pozitívnak (, a másik irány negatív lesz ).
Így a törvény rendkívül elegáns lesz:
egy csomópontból kifolyó áramok összege nulla.
\[ \sum{ I_i } = 0 \text{ A}\]Ez a képlet azt fejezi ki, hogy egy csomópontban nem keletkeznek és nem tűnnek el töltések. Megjegyzem, nem csak csomópontra, hanem áramköri részletre is igaz.
Ezt a törvényt Kirchhoff Gustav Robert [1824..1887=63] német fizikus, kémikus, mérnök, matematikus írta le.
![[ html: Kirchhoff Gustav Robert https://hu.wikipedia.org/wiki/Gustav_Robert_Kirchhoff ]](../_/html.gif)

Róla lett elnevezve, mint Kirchhoff I. törvénye. Ez szép, de mire jó?
Első példának legyen egy csillárkapcsolás. Két izzó ( L1. L2 ), mindkettő egymástól függetlenül kapcsolható ( K1, K2 ).
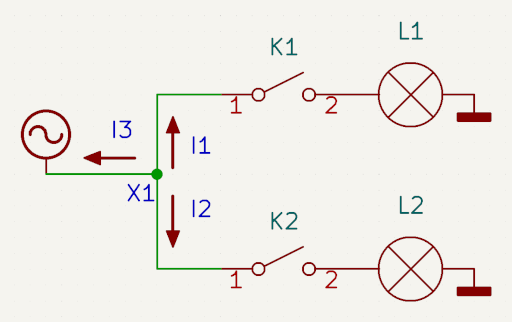
Feladat az áramerősségek kiszámolása. Feszültség U = 230 volt, az egyik izzó P1 = 60 wattos, a másik P2 = 40 wattos.
\[I_1 = \dfrac{P_1}{U} = \dfrac{60 \text{ W}}{230 \text{ V}} = 260,9 \text{ mA}\] \[I_2 = \dfrac{P_2}{U} = \dfrac{40 \text{ W}}{230 \text{ V}} = 173,9 \text{ mA}\]Kirchhoff I. törvénye X1 csomópontból kifolyó áramokra:
\[ I_1 + I_2 + I_3 = 0 \text{ A}\] \[ I_3 = -I_1 - I_2 \]| K1 | K2 | I1 | I2 | I3 |
| ki | ki | 0 A | 0 A | 0 A |
| ki | be | 0 A | 173,9 mA | -173,9 mA |
| be | ki | 260,9 mA | 0 A | -260,9 mA |
| be | be | 260,9 mA | 173,9 mA | -434,8 mA |
Figyeld meg, míg I1 és I2 kifelé folyik, ezért pozitív, I3 áram a csomópontba befolyik, azért negatív.
Itt elkalandozhatnék a gráfok
![[ html: gráf https://hu.wikipedia.org/wiki/Gr%C3%A1f ]](../_/html.gif)
 világába, ami csomópontok, köztük lévő élek leírásával foglalkozik, de mindkettőnek jobb, ha most ezt nem teszem meg.
világába, ami csomópontok, köztük lévő élek leírásával foglalkozik, de mindkettőnek jobb, ha most ezt nem teszem meg.
Másik példában legyen egy T csomópont, hozzákapcsolódó B, C, E vezetékekkel.
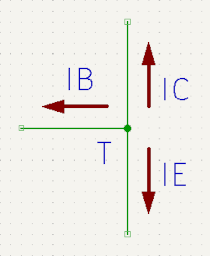
Ha IB = -1,5 milliamper és IC = 63*IB a kifolyó áramerősség ( azaz befelé folyik áram ), akkor mennyi IE?
\[ I_B + I_C + I_E = 0 \text{ A}\] \[ I_E = -I_B - I_C = -I_B - 63\cdot I_B = -64 \cdot I_B = -64 \cdot (-1,5 \text{ mA}) = 96 \text{ mA}\]A pozitív előjel azt jelenti, hogy E vezetéken a csomópontból kifelé folyik áram.
Az első részben már említettem a feszültség meghatározásánál, ha egy töltést egy másik töltés elektromos mezőjében A pontból B pontba mozgatok, a befektetett munka csak a végpontoktól függ, a ténylegesen bejárt pályától nem. Az ilyen mezőket konzervatív mezőnek nevezik és értelmezhető rajta potenciál, itt feszültség.
A próbatöltésemet az A pontból elviszem B pontba, majd B-ből egy másik pályán vissza A-ba. A körút után a befektetett energia nyilvánvalóan nulla, bármely pályára. Jól rímel az energiamegmaradás törvényére. Különösen, ha elkerülöm a fekete lyukakat és nem tart milliárd évekig a túra.
Képzeld el, ha egy körúton végigmenve magasabb potenciálon ( feszültségen ) találnám magam, az így nyert energiával tudnám fűteni a szobámat.
Escher Maurits Cornelis
![[ html: Maurits Cornelis Escher https://hu.wikipedia.org/wiki/Maurits_Cornelis_Escher ]](../_/html.gif)
 rajzolt ilyen körutat:
rajzolt ilyen körutat:

Tapasztalat szerint ilyen nincs.
Bevezetem a \(U_{AB}=U_A-U_B\) jelölést, így két pont között potenciálokkal, feszültségekkel írva:
\[\left(U_A-U_B\right)+\left(U_B-U_A\right)=0\text{ V}\] \[U_{AB} + U_{BA} = 0 \text{ V}\]Több pontot is beiktathatok a körútba, például A B C D és vissza A:
\[\left(U_A-U_B\right)+\left(U_B-U_C\right)+\left(U_C-U_D\right)+\left(U_D-U_A\right)=0\text{ V}\] \[U_{AB} + U_{BC} + U_{CD} + U_{DA} = 0 \text{ V}\]A hurokban az elektromotoros feszültségek ( Ue, feszültségforrások, áramforrások ) előjeles összege megegyezik a többi részen eső feszültségek ( Ut ) előjeles összegével.
\[ \sum{ U_e } = \sum{ U_t }\] \[ \sum{ U_t } - \sum{ U_e } = 0 \text{ V}\]Elegánsabban: bármely zárt hurokban a részfeszültségek összege nulla.
\[ \sum{ U_i } = 0 \text{ V}\]Azzal a kiegészítéssel, hogy feszültségforrások, áramforrások feszültségét fordítva kell figyelembe venned.
Ha van egy kapcsolásom és egy abban lévő hurok részfeszültségeire felírhatom Kirchhoff 2. törvényét. Egyszerűség kedvéért csak egy telepet, két LED-et és egy ellenállást kötök össze sorba, hurokba. Választok egy tetszőleges körüljárási irányt. Kétféleképpen tudok választani, vagy sikerül eltalálom, hogy a fogyasztókon a feszültség iránya megegyezzen az áramok irányával, vagy nem.
Szupererőm van, nem félek elosztani két negatív számot Ohm törvényénél:
\[R = \dfrac{U}{I} = \dfrac{-U}{-I}\]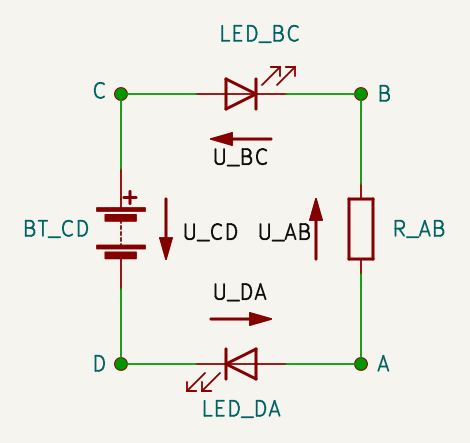
Néhány részfeszültséget tudok. LEDBC piros, LEDDA zöld, a telep lapos.
\[U_{BC} = -1,4 \text{ V}\] \[U_{CD} = -(-4,5 \text{ V}) = 4,5 \text{ V}\] \[U_{DA} = -1,6 \text{ V}\]Ebből ki tudom számolni \(U_{AB}\)-t.
\[U_{AB} = -U_{BC} - U_{CD} - U_{DA} = 1,4\text{ V} -4,5 \text{ V} +1,6 \text{ V} = -1,5 \text{ V}\]Ez azért nagyon jó nekem, mert ha megadom, hogy az áramkörben I = -5 milliamper folyjon, természetesen a választott körüljárási iránynak megfelelően, akkor ráolvasva Ohm törvényét ki tudom számolni az ellenállás értékét.
\[R_{AB} = \dfrac{U_{AB}}{I} = \dfrac{-1,5 \text{ V}}{-5 \text{ mA}} = 300 \text{ Ω}\]Jó lesz oda 330 Ω is :) A csomó negatív előjel annak köszönhető, hogy éppen így választottam meg a körüljárási irányt. Így a telep feszültségkülönbsége most pozitív, a terheléseken a feszültségkülönbség és az áramerősség negatív.
Egy másik hurok, egyszerűbb, az előzőtől abban különbözik, hogy a körüljárási irány maradt, de a telepet megfordítottam. A fogyasztókon folyó áramirány így megegyezik a rajtuk mérhető feszültségkülönbséggel.
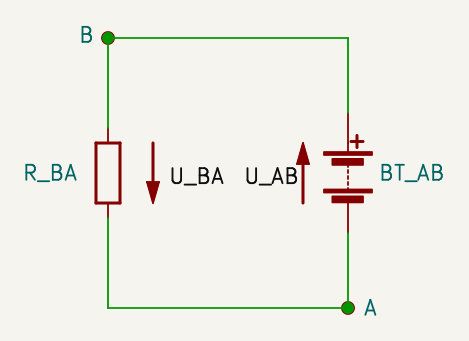
Most az ellenálláson eső feszültséget tudom:
\[U_{BA} = 4,5 \text{ V}\]Mekkora a telep feszültsége?
\[U_{AB} = - U_{BA} = -4,5 \text{ V}\]Telep polaritását a telep sarkainak feszültségkülönbségéhez képest fordítva kell felvennem.
A csomóponti törvény áramokról mond valamit, a csomópont feszültségéről semmit. Bármekkora lehet.
Feszültségekről a huroktörvény szól, a hurok egyes részein folyó áramerősségekről semmit nem állít. Bármekkorák lehetnek.
Csak rövid bevezetőt írtam neked, javaslom, keress Kirchhoff-törvényekre gyakorló példákat az interneten.
Természeti törvénynél is tudnom kell, milyen feltételek között érvényes, mikor használhatom. Ha olyan körülmények között használom, ami kívül esik hatáskörén, vagy magamat csapom be, vagy másokat. Kirchhoff egyenárammal tuti működik.
Váltakozóáramnál figyelembe kellhet venned, hogy egy vezetéknek induktivitása is van, két vezetéknek pedig kapacitása egymás között. Az, hogy ez mennyire elhanyagolható, azaz Kirchhoff mennyire pontos, a frekvenciától és az áramkör fizikai kialakításától függ.
Váltakozóáram gyorsuló töltést jelent, a gyorsuló töltés pedig elektromágneses mezőt hoz létre, energiát sugároz. Elvben váltakozóáramra nem működik, a gyakorlatban nagyon pontos, jól használható, ha az alkatrészek fizikai mérete sokkal kisebb, mint a váltakozó áramnak megfelelő elektromágneses ( rádió ) hullám hullámhossza. Antennát ne Kirchhoffal számolj... Másrészt ha az áramköröd környezetében elektromágneses mező van, például egy rádiótelefon, akkor az áramot indukál az áramkörödben, borítva mindent.
Rövid bevezető a rádiózásba #1
Experiment is the sole judge of scientific “truth”.
A (természet)tudományos igazság kizárólagos kritériuma a kísérlet.
Feynman Richard
![[ html: Feynman http://hu.wikipedia.org/wiki/Richard_Feynman ]](../_/html.gif)


 HG9IEG
Visszajelzés:
HG9IEG
Visszajelzés: